Proving physically universal negatives?

Let’s discuss this. A universal negative is an assertion of this form or similar to it …”There are no blah blah blah”, “There is no blah blah blah”.
For example, the statement … “There is no such thing as a unicorn”, or “Unicorns do not exist”. You can form your universal negative statement if you like.

Are there really no unicorns? What is the proof of that? Well you can say, I have never seen one. That means they do not exist.

That is rather subjective isn’t it. I mean you use your experience as the arbiter of objective reality?
What if we ask, what investigations did you do to conclude there are no unicorns. Well, you might say I have looked here or there and never found one. Could it be you just looked at the wrong place?
Isn’t it possible when you looked at it in a certain spot, the animal might have moved, and you just got unlucky?

Many scientists and especially physicists from what I can gather agree … it is impossible to prove universal negatives, physically.

It is because of human finiteness – we are not able to exhaust turning every stone on earth to check if a unicorn could be hiding in there.

Here is his argument.

Amazingly, I just read the other day a professor of philosophy said otherwise ( I am witholding his name as that is besides the point), meaning he can prove that unicorns do not exist. The argument goes this way.

He uses modus tollens. It looks this way, start from P implies Q, prove NOT Q, conclude NOT P. See below.

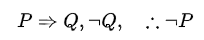
Proceeding he reasoned below:

1.) if unicorns exist, then we should have seen them in the fossil records?
2.) we do not see them in fossil records
3.) Therefore, unicorns do not exist.

Step 2 is the modus tollens., allowing us to conclude 3.). Hang on but wait. Is 1.) True? Yes right now the fossil records do not show any unicorn creatures, but are the fossil records now closed? Isn’t it true that as of today, you can still discover fossils of animals we currently do not see roaming around?
Read an example of the so called Protemnodon Viator – a giant kangaroo, just recently discovered. See below.

Researchers Find Fossils of Three Extinct Giant Kangaroo Species

I am afraid, the professor’s claim fails. Assumption in step 1, is false. Thus, step 3 does not follow.

In reality, universal negatives are only provable in mathematics.

For example, we can prove there are no prime numbers between 2 and 3. One property of a prime number is that it is a whole number and clearly there are no whole numbers between 2 and 3.

As for myself, I do not believe in unicorns not because I have no physical evidence of them. I do not believe in unicorns because of its reputation of being a mythical creature, not because I have proven it physically. Correct, I am banking on faith, that my faith in the fact that it is a mythical creature is true.

Thankfully, my eternal destiny does not hinge on my faith or lack of faith in unicorns existing, but some universal negatives though are not like that.

Deep Learning Example in R + torch/luz

This is more of a notes to self, to make me recall what I did to execute a simple DL exercise using torch and luz R packages.

The inspiration for this is from the video of Dr Bharatendra Rai using R and Keras. I am doing the same but using torch+luz. Here we use a Cardio dataset which I think originally comes from here. I am not familiar with the features and we are just going to use the last column (NSP) to predict but the other columns before that, as predictors. Here is an example of the data and note that NSP is actually a category data though it is numericcally represented by 1, 2, 3 as we see here.

Here is the view of the code

# YouTube link: https://youtu.be/XVfn6IpoUPU
#install.packages("keras")
library(torch)
library(torchvision)
library(luz)

# Get the data
# Data
#data <- read.csv('data/Cardiotocographic.csv', header=T)
data <- read.csv('https://raw.githubusercontent.com/bkrai/DeepLearningR/master/Cardiotocographic.csv', header=T)
# We will predict NSP, which is a categorical variable so we need to 
# Prepare it for one-hot-encoding it has to be base 0
head(data) # let's view the data
#data$NSP <- data$NSP - 1 # this is the base 0 for categories
# Let's view the data to see the distribution
barplot(prop.table(table(data$NSP)),
        col = rainbow(3),
        ylim = c(0, 0.8),
        ylab = 'Proportion',
        xlab = 'NSP',
        cex.names = 1.5)
#make categorical NSP
cardio_ds <- dataset (
  name = "CardioToCO",
  
  initialize  = function(input){
    input$NSP <- as.factor(input$NSP) # we need to make sure the categorical data to be predicted is a factor, here it is not so we ensure it to be so
    input$NSP <- as.integer(input$NSP)
    input <- as.matrix(input)
    dimnames(input) <- NULL 
    input [,1:21] <- scale(input[,1:21])
    # there is assumption that the dataset will have an x part - the predictor features and a y part that has the target feature to predict
    self$x <- torch_tensor(input[,-22])
    self$y <- torch_tensor(input[, 22], dtype = torch_long()) # the target to be predicted should be long or we will not get an error on data type.
    
  },
  
  .getitem = function(index){
    x<- self$x[index,]
    y<- self$y[index]
    list(x,y)
    
  },
  
  .length = function(){
    self$y$size()[[1]]
    
  }
  
)
# We must convert the dataframe into a matrix - for Keras Tensor Flow?


patient <- cardio_ds(data)

# partition the data into training and test
set.seed(1234)
train_ind <- sample(1:length(patient), size = 0.7 * length(patient))
train_ds <- dataset_subset(patient, indices = train_ind )

test_ind <- sample(setdiff(1:length(patient),train_ind) ,size = 0.3*length(patient))
test_ds <- dataset_subset(patient, indices = test_ind )


train_dl <-dataloader(train_ds, batch_size = 21,  shuffle = TRUE)
test_dl <-dataloader(test_ds, batch_size = 21)
# Create sequential model and add layers 
#
# define the model
net = nn_module(
  "class_net",
  
  initialize = function(d_in, d_hidden, d_out){
    
      self$net <- nn_sequential(
      nn_dropout(0.5),
      nn_linear(d_in, d_hidden),
      nn_relu(),
      nn_linear(d_hidden, d_out)
              , nn_softmax(2)
    )
  },
  
  forward = function(x){
    
    self$net(x)
    
  }
  
)

d_in <- 21
d_hidden <- 8
d_out <- 3
mymodel <- net (d_in, d_hidden, d_out)

fitted <- net |> 
  setup( 
    loss = nn_nll_loss(),
    optimizer = optim_adam
    ) |>
  set_hparams(d_in = d_in, d_hidden = d_hidden, d_out = d_out ) |>
  #fit (train_dl, epochs = 40, valid_data = test_dl)
  fit (train_ds, epochs = 40)
# let's plot the loss function as tracked 
print(plot(fitted))
#to predict 
predictions <- predict(fitted, test_ds)
# We are dealing w a categorical prediction so let's get the one that has the most probability we use torch_argmax
fitted |> evaluate(test_ds)
pred <- predictions |> apply(1, FUN = torch_argmax)
# we need to translate the predictions to the category indexes
giveInt <- function (x) {as.integer(x)}
  
 
#newpred <- function () {
#    temp <- c()
#    for (i in 1:length(pred)){
#      temp <- append(temp, giveInt(pred[[i]]))
#    }
#   return(temp)
#  }

# As we said we do not do for loops so here is the substiture code

#Unlist and clean up the predictions 
newpreds <- lapply(pred, FUN = function(x) append(temp, giveInt(x)))

mypreds <- unlist(newpreds)
# Get back the test data from the ds tensors
test_y <- test_ds$dataset$y[test_ds$indices] |> as.integer()

# present the confusion matrix to view
print(table (mypreds, test_y))

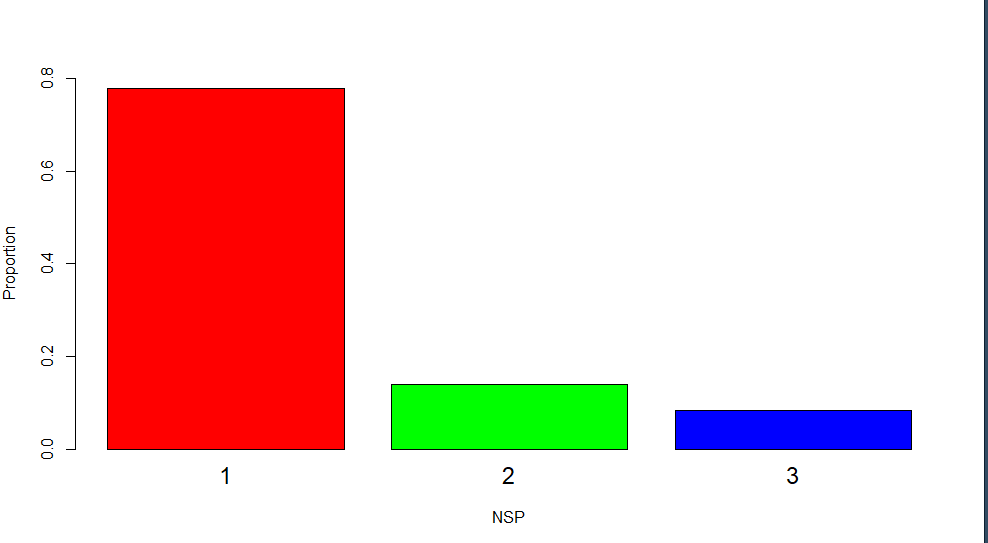
Here is the distribution of the NSP variable

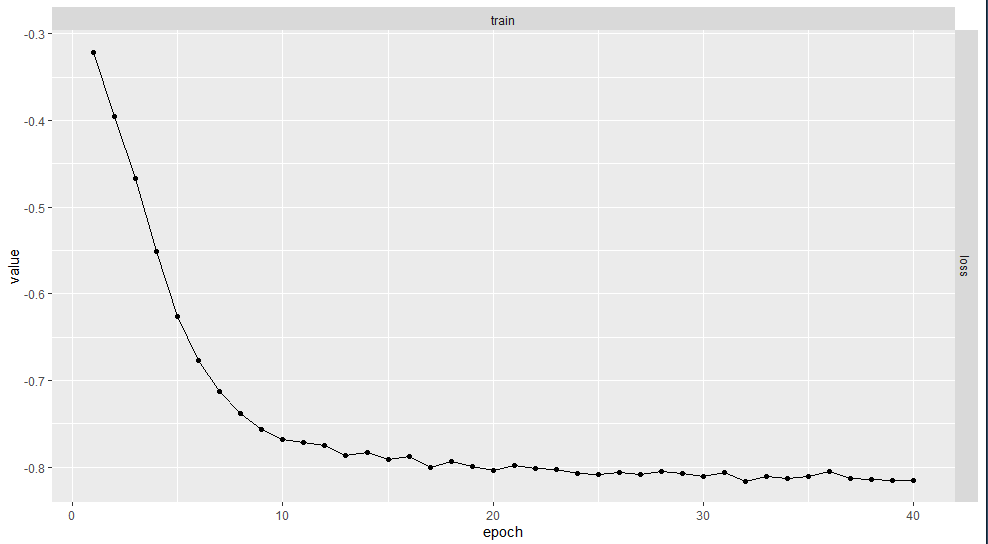
Here is how we see the loss function decreasing as we go through the epochs. Looks like it can be further improved by increasing it more than 40.

The confusion matrix we get. Not bad, about 87% accuracy. It can be improved by increasing the epoch size etc.

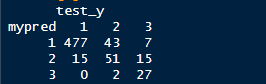
There it is. It complies with the data distribution of NSP, a good validation sanity check.

If you found this short tutorial helpful please let me know, and like and share.

R’s functional mission

From the start, one of the design preferences of R is to be faithful to the functional programming paradigm. One such philosophy is to make variables immutable. Mutability can produce confusion when the programmer is debugging.  Here is an example where R implements that policy of immutability when it comes to aliasing. Aliasing is a technique of naming a variable w another variable with the behaviour of one mimicked in the other. Implied aliasing does not work in R. You will have to explicitly call into your variables aliasing if you want that to happen. We compare how R prevents this compared to Python.

Let’s create a vector first, which we will turn to a list.

Let’s check its type, then turn it to a list, after that check its contents.

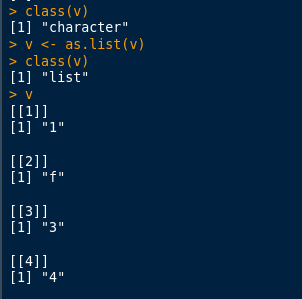
Let’s now assign v to ww.

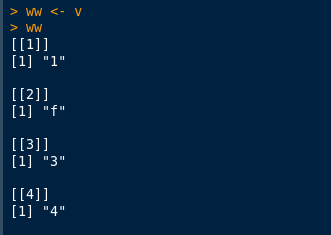
Now let’s target that “f” sitting in position [[2]] to 2 as after all that seems to be what is intended.

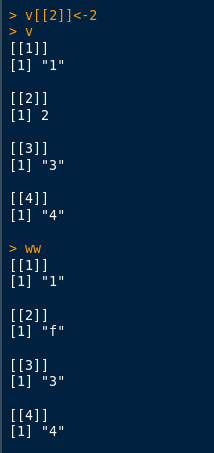
We can see that there was no change that happened to ww.

Let’s do this in Python. Here we use L for v and LL for ww.

We can see here that we changed LL but this was side-effected to L. In functional programming, side-effects are to be avoided. Sometimes, for an intended result, side-effects may be desirable for convenience but it has the tendency of messing up the train of thought of the programmer not familiar with the program that has it.

I don’t do for-loops

I have been programming now in R for at least 7 years and never once have I needed to resort to a for-loop. In fact I also never resort to while or until loops

I have always managed to avoid it with the apply family of functions.

Then today, I was defining a function with two variables where one of them has to be a regex. Instead, of calling it from the outside and passing these, I “curried” it and I felt good about it.

Now, if you know what I meant by that, then you are a functional programmer who will very likely be happy with R, but if you don’t see what I mean, I can see why you will pooh-pooh R, I get it, it is not for you.

Fixpoint Programming in R (recursion without recursing)

Fibonacci Spiral Jahobr, CC0, via Wikimedia Commons

This is the last part of my notes on recursion. I am reminded that these techniques are only possible in a language that is supportive of the functional style of programming. Fixpoint is a mathematics concept which has been migrated to computer science.

In mathematics, a fixpoint refers to a function. Well, what a surprise, we are talking about functional programming after all! Here is a quick way of explaining a fixpoint of a function. Given a function , the fixpoint of this function is that value of for which this equation holds . We illustrate it below. The fixpoints of the function below are 0 and 1.

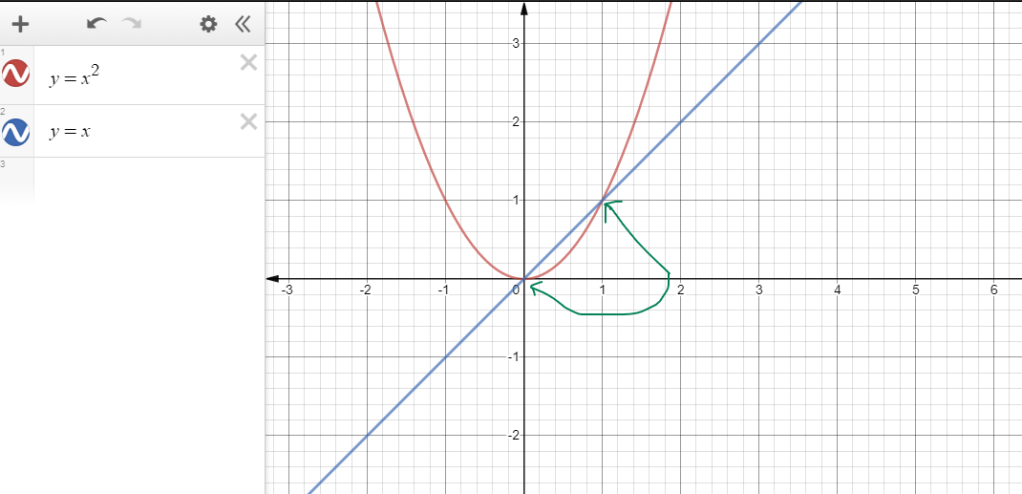
In Calculus and in functional programming this is called the Y-Combinator. This was discovered by the American computer scientist Haskell Curry. For those who are into this calculus, it is stated below like this:

Fixpoint programming allows you to effect a recursion without doing an actual recursion. It relieves you of complexities that come with recursion.

In Scheme, it is so close to the above and gives you an almost one to one correspondence:

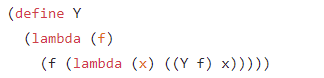
Watch how this is directly translatable to R:

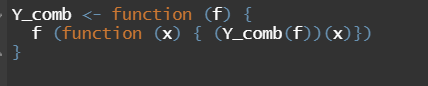
This is why I have so much fun with R. It looks so like Scheme!

Now let us do the Fibonacci Sequence without Tail Recursion! This version is what comes naturally – it is recursion but it is not tail recursion by definition. It is because the last thing it does is not call the function, instead, it adds two results.

We now pass this function to our Y-Combinator and voila! It works!

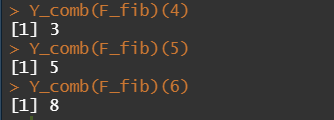
You can keep this R Y-Combinator function in your pocket, you can carry it with you anywhere and bring it up when you need to use it. It is forever done and should always work.

For now, this ends my rambling on recursive programming in R.

Continuous Passing Style, Tail Call and the λ Function

Last time I wrote some notes to self on the use of Tail Recursion in R. What I gave in the previous post (look at the one before this) was actually the accumulator passing style to do a tail call. Today I will do the same, this time the so called CPS. Again, I will illustrate using the Fibonacci Sequences.

Fibonacci Spiral by Jahobr, CC0, via Wikimedia Commons

Continuous Passing Style of recursion is a type of recursion where you look at computation in two senses. Past Tense – the part of computation that have already been completed and that part that is still yet to do. In CPS, on the latter part the programmer passes this as a complete parameter that needs to be executed. This parameter is called the continuation, semantically – you are saying do some more.

This is where the concept of the lambda function, I think becomes very handy. The so called anonymous function – or function on the fly is the way to go. Did you know that R – follows closely the syntax of the λ calculus? See the examples below:

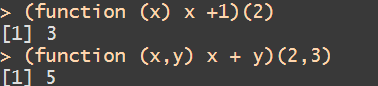
The function command in R is the lambda operator. We can translate the above this way:

⇒ 3

⇒ 5

Anyway, as I was saying, we get the same now w/ CPS + tail call with the help from and we get this (refer to the previous post!)

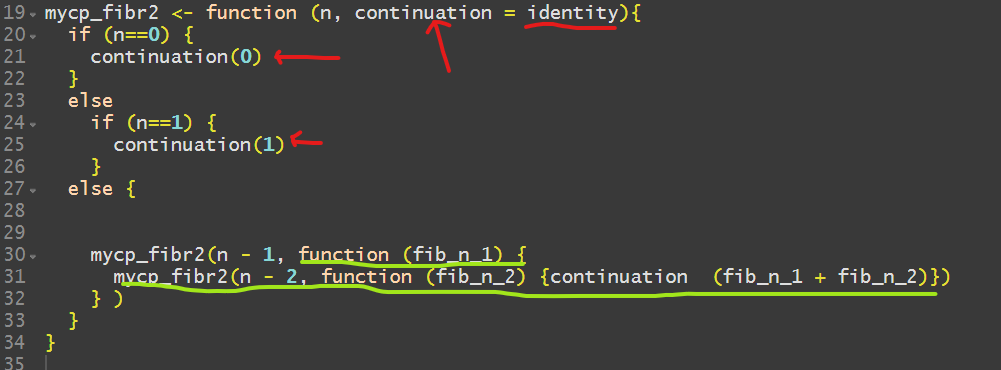
Notice now we have an extra parameter – which we conveniently call continuation (which could have been any name we wished) but note! It is equal to the identity function found in R. The identity function returns the same thing we pass to it. See line 21 and 25. Note that in line 30, the text I underlined in green stands for the continuation work that needs to be done – a bit requiring some reflection because it is a curried function.

Note another idea – I am calling the recursive function deep again inside it. Here is the result

You might say – hmm, that code looks wild, it looks like voodoo to me. We can re-write it a bit better so here is another version:

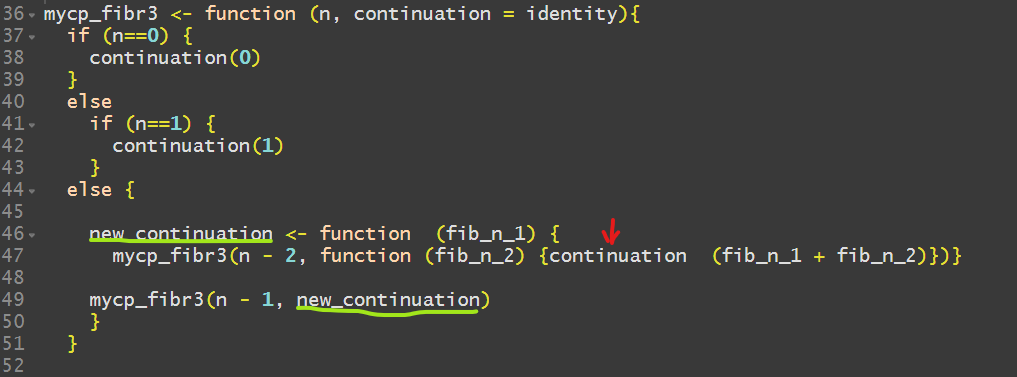
In line 46-47, I re-arranged the code so it can be better analyzed. The we now have a name for the lambda.

I marked with a red arrow the continuation command for deeper thought. Here is the result of execution…It works!

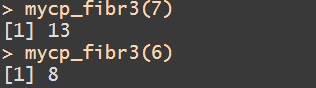
So note, again, we are indeed doing tail recursion here because, the last thing we are doing is we cleanly call back ourselves.

Functional programming is not popular because it seems to suggest you need to learn a few more conventions on top of the language but for me, it does wind up more elegant in the end.

Let me know if you have any suggestions or any topic you would like me to tackle next time.

Doing Tail Recursion in R

I have been reflecting on recursion lately and as far as I know, tail recursion is the best kind of recursion and is the way to go in R. However, I heard R’s interpreter does not optimize recursion, which is sad. At least, it does help you not to blow up your call stack. There are several ways of handling this:

• By using Trampolines. However, this is not straight forward and can be messy for some. It is not intuitive.
• By using type of continuation passing function definition. There is a gist of this in here by a great R author Thomas Mailund who wrote the book Functional Programming in R.-

In this post, I shall follow Mailund’s recommendation of how to do tail recursion in R, but I will do this using the Fibonacci Sequence rather than the usual Factorial example to illustrate recursion.

Mathematically, the Fibonacci Sequence is formulated this way:

and

Here are a few leading sequences etc.

Following the mathematical form, we get this R code which reminds you of the C syntax:

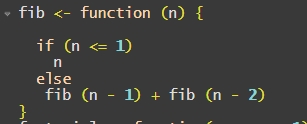
The definition of tail recursion is that the last thing your recursion should do is to do nothing else except to call the function again. Although this follows neatly the mathematical form, this is not doing tail recursion.

The reason is that it is not simply calling the function, it does something more. It does call the function but it is adding the result of the calls. By definition, this is not tail recursion, it does not simply call the function. Non-tail recursion can blow up your call stack heap. So, you could be lucky or not so lucky as you do not know what might be when your function is called.

Below is the same version but legally does a tail recursion

Few things to observe. Notice now that we do not simply pass to the function. There are more arguments. are what is called accumulators. I know, it is not natural and it needs a bit more mental work than the non functional style. Note the {,}. I placed them there because for some reason the R version 4.0.3 will give me the error below if I do not put them there although legally it is not required by the syntax. Here is what I get if I don’t :

However, there is a certain cuteness in this code. Observe that the position is acting as , and the position is acting as .

In Lisp/Scheme programming parlance this is the concept of call by continuous passing.

Unlike in Scheme where tail recursion is so supported in the language, it is not so with R due to its dynamic nature. Maitlund has the tailr package that translates your tail recursion internally however, I won’t get into that here. My objective is the need to have lateral thinking when making your recursive call, tail recursive by the use of accumulators – it requires some creativity and some challenge, but it looks elegant to me in the end.

2 years old but still relevant today?

HT:

An opinion piece in the usual debate…

Why R and not Python for Data Science

Why Python is not for the future?

Python is a great programming language to learn if you are starting off in coding, but is this where you should end?

This is an interesting opinion on the usual debate…

Why Python is not the Programming Language of the Future

Why R is not likely to go down soon

I know why Python is becoming more popular than R. The syntax can be grasp by kids. Whereas R needs a professional computer scientist’s mind to appreciate it. It is functional programming friendly and that demands thinking out of what is obvious box.

Also, I get that the switch to Python promises a hopeful career to the IT professional.

However, for old folks like me who is no longer after a career uplift, I will stick to R if not professionally at least privately because it is the RIGHT language to use.

Here is a study why R is not likely going to disappear so soon, at least those who are doing real data science – those in the health sciences.

https://www.datasciencecentral.com/profiles/blogs/which-one-is-faster-in-multiprocessing-r-or-python